设四面体的六条棱的长分别为 $1,1,1,1,\sqrt 2$ 和 $a$,且长为 $a$ 的棱与长为 $\sqrt 2$ 的棱异面,则 $a$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2012年高考重庆卷(理)
【标注】
【答案】
A
【解析】
设在四面体 $P-ABC$ 中,$$PA=PB=AC=BC=1,AB=\sqrt 2,PC=a,$$设 $AB$ 中点为 $D$,则$$PD=CD=\dfrac {\sqrt 2}{2},$$将面 $PAB$ 沿棱 $AB$ 翻转,则 $0<a<\sqrt 2$.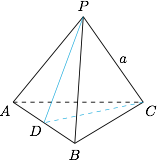

题目
答案
解析
备注