高为 $\sqrt 2 $ 的四棱锥 $S - ABCD$ 的底面是边长为 $1$ 的正方形，点 $S$、$A$、$B$、$C$、$D$ 均在半径为 $1$ 的同一球面上，则底面 $ABCD$ 的中心与顶点 $S$ 之间的距离为 \((\qquad)\)
【难度】
【出处】
2011年高考重庆卷（文）
【标注】
【答案】
A
【解析】
如图：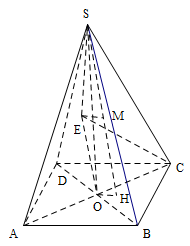
设四棱锥 $S - ABCD$ 的外接球球心为 $E$，则 $OE \perp $ 面 $ABCD$．
在 $\mathrm{Rt} \triangle EOC$ 中，$EC = 1$，$OC = \dfrac{{\sqrt 2 }}{2}$，
$ \therefore $ $EO = \sqrt {E{C^2} - O{C^2}} = \dfrac{{\sqrt 2 }}{2}$．
$ \because $ 四棱锥 $S - ABCD$ 的高 $SH = \sqrt 2 $，
$ \therefore $ $OE = \dfrac{1}{2}SH$，$OE\parallel \dfrac{1}{2}SH$．
过 $E$ 作 $EM \perp SH$ 交 $SH$ 于 $M$，
则 $SM = \dfrac{{\sqrt 2 }}{2}$．
在 $\mathrm{Rt} \triangle SEM$ 中，$ES = 1$，
则 $EM = \sqrt {E{S^2} - S{M^2}} = \dfrac{{\sqrt 2 }}{2}$．
$ \therefore $ $OH = \dfrac{{\sqrt 2 }}{2}$，
$ \therefore $ $OS = \sqrt {O{H^2} + S{H^2}} = \sqrt {\dfrac{1}{2} + 2} = \dfrac{{\sqrt {10} }}{2}$．
设四棱锥 $S - ABCD$ 的外接球球心为 $E$，则 $OE \perp $ 面 $ABCD$．在 $\mathrm{Rt} \triangle EOC$ 中，$EC = 1$，$OC = \dfrac{{\sqrt 2 }}{2}$，
$ \therefore $ $EO = \sqrt {E{C^2} - O{C^2}} = \dfrac{{\sqrt 2 }}{2}$．
$ \because $ 四棱锥 $S - ABCD$ 的高 $SH = \sqrt 2 $，
$ \therefore $ $OE = \dfrac{1}{2}SH$，$OE\parallel \dfrac{1}{2}SH$．
过 $E$ 作 $EM \perp SH$ 交 $SH$ 于 $M$，
则 $SM = \dfrac{{\sqrt 2 }}{2}$．
在 $\mathrm{Rt} \triangle SEM$ 中，$ES = 1$，
则 $EM = \sqrt {E{S^2} - S{M^2}} = \dfrac{{\sqrt 2 }}{2}$．
$ \therefore $ $OH = \dfrac{{\sqrt 2 }}{2}$，
$ \therefore $ $OS = \sqrt {O{H^2} + S{H^2}} = \sqrt {\dfrac{1}{2} + 2} = \dfrac{{\sqrt {10} }}{2}$．
题目
答案
解析
备注
