已知三棱锥 $A-BCO$，$OA$，$OB$，$OC$ 两两垂直且长度为 $6$，长为 $2$ 的线段 $MN$ 的一个端点 $M$ 在棱 $OA$ 上运动，另一个端点 $N$ 在 $\triangle{BCO}$ 内运动（含边界），则 $MN$ 的中点 $P$ 的轨迹与三棱锥的面所围成的几何体的体积为 \((\qquad)\) 
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
注意到 $MO\perp$ 底面 $OBC$，于是 $MO\perp ON$，因此我们可以将两个动点 $M$，$N$ 间的距离为常数转化为定点 $O$ 到动点 $P$ 的距离为常数．
因此点 $P$ 的轨迹为以 $O$ 为球心的一个 $\dfrac 18$ 球面，如图．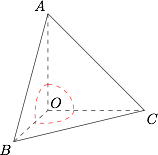
$\dfrac 18$ 球的体积为$$\dfrac 18\cdot \dfrac 43 \pi \cdot 1^3=\dfrac{\pi}{6},$$三棱锥的体积为 $36$，于是所求几何体的体积为 $\dfrac{\pi}{6}$ 或 $36-\dfrac{\pi}{6}$．
因此点 $P$ 的轨迹为以 $O$ 为球心的一个 $\dfrac 18$ 球面，如图．
$\dfrac 18$ 球的体积为$$\dfrac 18\cdot \dfrac 43 \pi \cdot 1^3=\dfrac{\pi}{6},$$三棱锥的体积为 $36$，于是所求几何体的体积为 $\dfrac{\pi}{6}$ 或 $36-\dfrac{\pi}{6}$．
题目
答案
解析
备注
