查看数据源：592699728044a0000a078cc1
在一个正方体 $ABCD-A_1B_1C_1D_1$ 中，$P$ 为正方形 $A_1B_1C_1D_1$ 四边上的动点，$O$ 为底面正方形 $ABCD$ 的中心，$M$，$N$ 分别为 $AB$，$BC$ 中点，点 $Q$ 为平面 $ABCD$ 内一点，线段 $D_1Q$ 与 $OP$ 互相平分，则满足 $\overrightarrow{MQ}=\lambda \overrightarrow{MN}$ 的实数 $\lambda$ 的值有 \((\qquad)\)
A: $0$ 个
B: $1$ 个
C: $2$ 个
D: $3$ 个
【难度】
【出处】
无
【标注】
  • 知识点
    >
    立体几何
    >
    空间位置关系
    >
    空间的平行关系
【答案】
C
【解析】
关键条件为“线段 $D_1Q$ 与 $OP$ 互相平分”，我们将其转化为“四边形 $OQPD_1$ 为平行四边形”，也即 $\overrightarrow{D_1O}=\overrightarrow{PQ}$．而条件“$\overrightarrow{MQ}=\lambda \overrightarrow{MN}$”即“$Q$ 在线段 $MN$ 上”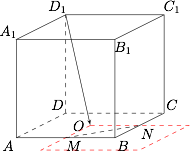．综合以上考虑，点 $Q$ 的位置为正方形 $A_1B_1C_1D_1$ 沿 $\overrightarrow{D_1O}$ 移动后与线段 $MN$ 的交点，显然只有 $M$，$N$ 两处，对应的实数分别为 $0$ 和 $1$．
题目 答案 解析 备注
0.110530s