在棱长为 $1$ 的正方体 $ABCD-A_1B_1C_1D_1$ 中，点 $P_1,P_2$ 分别是线段 $AB$，$BD_1$（不包括端点）上的动点，且线段 $P_1P_2$ 平行于平面 $A_1ADD_1$，则四面体 $P_1P_2AB_1$ 的体积的最大值是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
如图．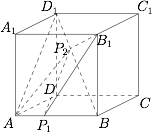
设 $BP_1=x$（$0<x<1$），则\[\begin{split}V_{P_1P_1AB_1}&=\dfrac 13 S_{\triangle{AP_1B_1}}\cdot d(P_2,ABB_1A_1)\\&=\dfrac 13 \cdot \dfrac 12(1-x)x\\&=\dfrac{x(1-x)}{6}\leqslant \dfrac 1{24},\end{split}\]当 $BP_1=\dfrac 12$ 时，等号成立．
设 $BP_1=x$（$0<x<1$），则\[\begin{split}V_{P_1P_1AB_1}&=\dfrac 13 S_{\triangle{AP_1B_1}}\cdot d(P_2,ABB_1A_1)\\&=\dfrac 13 \cdot \dfrac 12(1-x)x\\&=\dfrac{x(1-x)}{6}\leqslant \dfrac 1{24},\end{split}\]当 $BP_1=\dfrac 12$ 时，等号成立．
题目
答案
解析
备注
