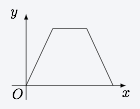
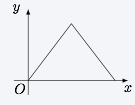
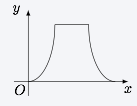
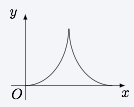
如图，动点 $P$ 在正方体 $ABCD-A_1B_1C_1D_1$ 的对角线 $BD_1$ 上．过点 $P$ 作垂直于平面 $BB_1D_1D$ 的直线，与正方体表面相交于 $M$、$N$．设 $BP=x$，$MN=y$，则函数 $y=f(x)$ 的图象大致是 \((\qquad)\) 
A:
B:
C:
D:
【难度】
【出处】
无
【标注】
【答案】
B
【解析】
将空间的问题转化为平面的问题，如图．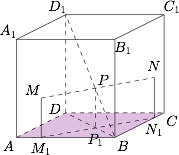
作 $MPN$ 在底面上的投影 $M_1P_1N_1$，则可以将 $MN$ 与 $BP$ 间的函数关系转化为 $M_1N_1$ 与 $BP_1$ 之间的函数关系加以考虑（由于 $\dfrac{BP}{BP_1}$ 为定值，因此相当于对函数图象作了一个伸缩变换，并不影响对图象形状的判断），在正方形 $ABCD$ 中，$M_1N_1$ 随着 $P_1$ 在 $BD$ 上的移动而移动，容易得到 $M_1N_1$ 与 $BP_1$ 之间的函数关系如选项B所示．
作 $MPN$ 在底面上的投影 $M_1P_1N_1$，则可以将 $MN$ 与 $BP$ 间的函数关系转化为 $M_1N_1$ 与 $BP_1$ 之间的函数关系加以考虑（由于 $\dfrac{BP}{BP_1}$ 为定值，因此相当于对函数图象作了一个伸缩变换，并不影响对图象形状的判断），在正方形 $ABCD$ 中，$M_1N_1$ 随着 $P_1$ 在 $BD$ 上的移动而移动，容易得到 $M_1N_1$ 与 $BP_1$ 之间的函数关系如选项B所示．
题目
答案
解析
备注
