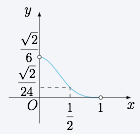
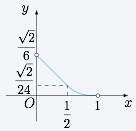
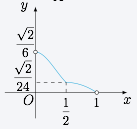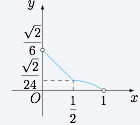如图，已知正四棱锥 $S-ABCD$ 所有棱长都为 $1$，点 $E$ 是侧棱 $SC$ 上一动点，过点 $E$ 垂直于 $SC$ 的截面将正四棱锥分成上、下两部分．记 $SE=x$（$0<x<1$），截面下面部分的体积为 $V(x)$，则函数 $y=V(x)$ 的图象大致为 \((\qquad)\) 
A:
B:
C:
D:
【难度】
【出处】
2012年高考江西卷（理）
【标注】
【答案】
A
【解析】
如下左图，将正四棱锥沿 $SC$ 方向竖直放置．
注意 $\triangle{SAC}$ 为等腰直角三角形，$BD$ 与 $SA$，$SC$ 均垂直．
取 $SC$ 的中点 $M$，连接 $BM$，$DM$，容易证明截面 $BDM$ 与 $SC$ 垂直．
下面分别研究 $E$ 在 $SM$ 段和 $MC$ 段时所求体积 $V$ 与 $x$ 的关系 $V(x)$．
不妨设 $\triangle{BDM}$ 的面积为 $a$，则正四棱锥 $S-ABCD$ 的体积为 $\dfrac 23 a$，组成它的三部分 $S-ABD$，$S-BDM$，$C-BDM$ 的体积分别为 $\dfrac 13 a$，$\dfrac 16 a$，$\dfrac 16 a$．
$1^{\circ}$ 在 $SM$ 段，如上中图，此时$$\dfrac{SSE_1}{SM}=2x.$$与点 $M$ 的位置类似，取 $SA$ 的中点 $N$，连接 $BN$，$DN$，则 $BDN$ 与 $SA$ 垂直，设 $FI$，$HG$ 与截面 $BDN$ 分别交于点 $P$，$Q$．于是\[\begin{split}&V_{AFH-SIG}=\dfrac{AS+FI+HG}{3}\cdot S_{\triangle{PQN}}=\dfrac{1+2(1-2x)}{3}\cdot(2x)^2\cdot a,\\ &V_{S-GIE_1}=\dfrac 13\cdot (2x)^2\cdot a\cdot x.\end{split}\]将二者代入，有$$V(x)=\dfrac 23 a-4ax^2(1-x).$$$2^{\circ}$ 在 $MC$ 段，如上右图，此时$$\dfrac{CE_2}{CM}=2(1-x).$$此时\[\begin{split}V(x)&=V_{C-JKE_2}\\ &=\dfrac 13[2(1-x)]^2\cdot a \cdot (1-x)\\ &=\dfrac 43 a(1-x)^3.\end{split}\]据此可以判断正确答案为A．
注意 $\triangle{SAC}$ 为等腰直角三角形，$BD$ 与 $SA$，$SC$ 均垂直．
取 $SC$ 的中点 $M$，连接 $BM$，$DM$，容易证明截面 $BDM$ 与 $SC$ 垂直．下面分别研究 $E$ 在 $SM$ 段和 $MC$ 段时所求体积 $V$ 与 $x$ 的关系 $V(x)$．
不妨设 $\triangle{BDM}$ 的面积为 $a$，则正四棱锥 $S-ABCD$ 的体积为 $\dfrac 23 a$，组成它的三部分 $S-ABD$，$S-BDM$，$C-BDM$ 的体积分别为 $\dfrac 13 a$，$\dfrac 16 a$，$\dfrac 16 a$．
$1^{\circ}$ 在 $SM$ 段，如上中图，此时$$\dfrac{SSE_1}{SM}=2x.$$与点 $M$ 的位置类似，取 $SA$ 的中点 $N$，连接 $BN$，$DN$，则 $BDN$ 与 $SA$ 垂直，设 $FI$，$HG$ 与截面 $BDN$ 分别交于点 $P$，$Q$．于是\[\begin{split}&V_{AFH-SIG}=\dfrac{AS+FI+HG}{3}\cdot S_{\triangle{PQN}}=\dfrac{1+2(1-2x)}{3}\cdot(2x)^2\cdot a,\\ &V_{S-GIE_1}=\dfrac 13\cdot (2x)^2\cdot a\cdot x.\end{split}\]将二者代入，有$$V(x)=\dfrac 23 a-4ax^2(1-x).$$$2^{\circ}$ 在 $MC$ 段，如上右图，此时$$\dfrac{CE_2}{CM}=2(1-x).$$此时\[\begin{split}V(x)&=V_{C-JKE_2}\\ &=\dfrac 13[2(1-x)]^2\cdot a \cdot (1-x)\\ &=\dfrac 43 a(1-x)^3.\end{split}\]据此可以判断正确答案为A．
题目
答案
解析
备注
