查看数据源：59269ce774a309000798cda0
已知矩形 $ABCD$，$AB=1$，$BC=\sqrt 2$．将 $\triangle{ABD}$ 沿矩形的对角线 $BD$ 所在的直线进行翻折，在翻折过程中 \((\qquad)\)
A: 存在某个位置，使得直线 $AC$ 与直线 $BD$ 垂直
B: 存在某个位置，使得直线 $AB$ 与直线 $CD$ 垂直
C: 存在某个位置，使得直线 $AD$ 与直线 $BC$ 垂直
D: 对任意位置，三对直线“$AC$ 与 $BD$”，“$AB$ 与 $CD$”，“$AD$ 与 $BC$”均不垂直
【难度】
【出处】
2012年高考浙江卷（理）
【标注】
  • 知识点
    >
    立体几何
    >
    空间位置关系
    >
    空间的垂直关系
    >
    三垂线定理
【答案】
B
【解析】
根据三垂线定理及其逆定理，可以将“线线垂直”等价转化为“线影垂直”，即若在翻折过程中存在某个位置使得直线 $a$ 与底面上的直线 $b$ 垂直，则存在某个位置使得直线 $a$ 在底面上投影与直线 $b$ 垂直．
如图1，在翻折过程中，$A$ 点在底面上的投影由 $A$ 变化到 $M$（$M$ 为 $A$ 关于直线 $BD$ 的对称点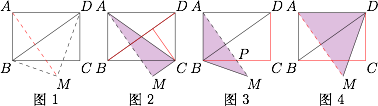）．对于选项A，由于直线 $AC$ 在底面上的投影从 $CA$ 到 $CM$ 变化过程中始终不与 $BD$ 垂直，错误；
对于选项B，直线 $AC$ 在底面上的投影为 $BP$ 时与 $CD$ 垂直，正确；
对于选项C，由于直线 $AD$ 在底面上的投影从 $DA$ 到 $DM$ 变化过程中始终不与 $BC$ 垂直，错误．
因此选B．
题目 答案 解析 备注
0.110583s