空间点到平面的距离定义如下：过空间一点作平面的垂线，这个点和垂足之间的距离叫做这个点到这个平面的距离．已知平面 $\alpha$，$\beta$，$\gamma$ 两两互相垂直，点 $A\in \alpha$，点 $A$ 到 $\beta$，$\gamma$ 的距离都是 $3$，点 $P$ 是 $\alpha$ 上的动点，满足 $P$ 到 $\beta$ 的距离是 $P$ 到点 $A$ 距离的 $2$ 倍，则点 $P$ 的轨迹上的点到 $\gamma$ 的距离的最小值是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
理解题意后如图建系，$A(3,3)$，$P(x,y)$．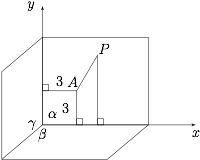
于是 $P$ 点的轨迹方程为$$y=2\sqrt{(x-3)^2+(y-3)^2},$$解得$$x=3\pm \dfrac{\sqrt 3}{2}\cdot \sqrt{4-(y-4)^2}.$$因此点 $P$ 的轨迹上的点到 $\gamma$ 的距离的最小值即 $x$ 的最小值为 $3-\sqrt 3$．
于是 $P$ 点的轨迹方程为$$y=2\sqrt{(x-3)^2+(y-3)^2},$$解得$$x=3\pm \dfrac{\sqrt 3}{2}\cdot \sqrt{4-(y-4)^2}.$$因此点 $P$ 的轨迹上的点到 $\gamma$ 的距离的最小值即 $x$ 的最小值为 $3-\sqrt 3$．
题目
答案
解析
备注
