点 $P$ 是棱长为 $1$ 的正方体 $ABCD-A_1B_1C_1D_1$ 的底面 $ABCD$ 上一点，则 $\overrightarrow{PA}\cdot \overrightarrow{PC_1}$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
如图．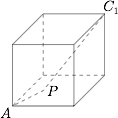
由极化恒等式可得\[\overrightarrow{PA}\cdot \overrightarrow{PC_1}=OP^2-\dfrac 14AC_1^2=OP^2-\dfrac 34,\]其中 $O$ 为正方体的中心．而 $OP$ 的取值范围是 $\left[\dfrac 12,\dfrac {\sqrt 3}2\right]$，于是所求的取值范围是 $\left[-\dfrac 12,0\right]$．
由极化恒等式可得\[\overrightarrow{PA}\cdot \overrightarrow{PC_1}=OP^2-\dfrac 14AC_1^2=OP^2-\dfrac 34,\]其中 $O$ 为正方体的中心．而 $OP$ 的取值范围是 $\left[\dfrac 12,\dfrac {\sqrt 3}2\right]$，于是所求的取值范围是 $\left[-\dfrac 12,0\right]$．
题目
答案
解析
备注
