正方体 $ABCD-A_1B_1C_1D_1$ 的棱长为 $1$，底面中心为 $O$，$A_1D_1,CC_1$ 的中点分别为 $M,N$，则三棱锥 $O-MB_1N$ 的体积为 \((\qquad)\)
【难度】
【出处】
2017年清华大学429学术能力测试数学试题
【标注】
【答案】
B
【解析】
如图，过 $O$ 作 $AB$ 的平行线，分别与棱 $AD,BC$ 交于点 $E,F$，连结 $BE$，并取 $BF$ 的中点 $Q$．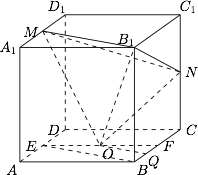
易知$$OQ\parallel BE\parallel B_1M,$$所以 $OQ\parallel $ 平面 $MNB_1$，故$$V_{O-MNB_1}=V_{Q-MNB_1}=V_{M-NQB_1}.$$又因为\[\begin{split}S_{\triangle{NQB_1}}&=S_{BCC_1B_1}-S_{\triangle{NC_1B_1}}-S_{\triangle{QNC}}-S_{\triangle{QBB_1}}\\&=1-\dfrac 14 -\dfrac 3{16}-\dfrac 18 \\&=\dfrac 7{16},\end{split}\]故$$V_{Q-MNB_1}=\dfrac 13 S_{\triangle{NQB_1}}\cdot A_1B_1=\dfrac 7{48}.$$
易知$$OQ\parallel BE\parallel B_1M,$$所以 $OQ\parallel $ 平面 $MNB_1$，故$$V_{O-MNB_1}=V_{Q-MNB_1}=V_{M-NQB_1}.$$又因为\[\begin{split}S_{\triangle{NQB_1}}&=S_{BCC_1B_1}-S_{\triangle{NC_1B_1}}-S_{\triangle{QNC}}-S_{\triangle{QBB_1}}\\&=1-\dfrac 14 -\dfrac 3{16}-\dfrac 18 \\&=\dfrac 7{16},\end{split}\]故$$V_{Q-MNB_1}=\dfrac 13 S_{\triangle{NQB_1}}\cdot A_1B_1=\dfrac 7{48}.$$
题目
答案
解析
备注
