在 $\triangle ABC$ 中，$\angle A=60^\circ$，$\angle B=45^\circ$，$\angle A$ 的角平分线长度为 $2$，$CH\perp AB$ 于 $H$，则下列正确的是 \((\qquad)\)
【难度】
【出处】
2017年清华大学429学术能力测试数学试题
【标注】
【答案】
ABC
【解析】
如图，设 $\angle A$ 的角平分线为 $AD$．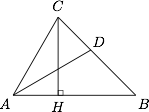
根据题意，有\[\angle CAD=\angle BAD=30^\circ,\angle HCB=45^\circ,\angle ADC=75^\circ,\]于是\[AC=AD=2,\]进而\[CH=AC\cdot \sin\angle CAH=\sqrt 3,\]选项 A 正确．
进而\[BH=CH=\sqrt 3,\]因此\[AB=AH+BH=\sqrt 3+1,\]选项 B 正确．
进而\[BC=\sqrt 2 BH=\sqrt 6,\]选项 C 正确．
进而\[S_{\triangle ABC}=\dfrac 12\cdot AB\cdot CH=\dfrac 12\cdot \left(\sqrt 3+1\right)\cdot \sqrt 3=\dfrac{3+\sqrt 3}3,\]选项 D 错误．
根据题意，有\[\angle CAD=\angle BAD=30^\circ,\angle HCB=45^\circ,\angle ADC=75^\circ,\]于是\[AC=AD=2,\]进而\[CH=AC\cdot \sin\angle CAH=\sqrt 3,\]选项 A 正确．进而\[BH=CH=\sqrt 3,\]因此\[AB=AH+BH=\sqrt 3+1,\]选项 B 正确．
进而\[BC=\sqrt 2 BH=\sqrt 6,\]选项 C 正确．
进而\[S_{\triangle ABC}=\dfrac 12\cdot AB\cdot CH=\dfrac 12\cdot \left(\sqrt 3+1\right)\cdot \sqrt 3=\dfrac{3+\sqrt 3}3,\]选项 D 错误．
题目
答案
解析
备注
