直线 $2x + y - 10 = 0$ 与不等式组 ${\begin{cases}
x \geqslant 0, \\
y \geqslant 0, \\
x - y \geqslant - 2, \\
4x + 3y \leqslant 20 \\
\end{cases}}$ 表示的平面区域的公共点有 \((\qquad)\)
x \geqslant 0, \\
y \geqslant 0, \\
x - y \geqslant - 2, \\
4x + 3y \leqslant 20 \\
\end{cases}}$ 表示的平面区域的公共点有 \((\qquad)\)
【难度】
【出处】
2011年高考湖北卷（文）
【标注】
【答案】
B
【解析】
画出不等式组表示的区域，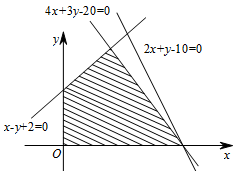
直线 $2x + y - 10 = 0$ 与其只有一个公共点．
直线 $2x + y - 10 = 0$ 与其只有一个公共点．
题目
答案
解析
备注
