已知向量 $ {\overrightarrow {a}}=\left(x+z,3\right)$，${\overrightarrow {b}}=\left(2,y-z\right) $，且 $ {\overrightarrow {a}}\perp {\overrightarrow {b}} $．若 $ x$，$y $ 满足不等式 $ |x|+|y|\leqslant 1 $，则 $ z $ 的取值范围为 \((\qquad)\)
【难度】
【出处】
2011年高考湖北卷（理）
【标注】
【答案】
D
【解析】
因为 $\overrightarrow a\perp \overrightarrow b $，所以 $ 2\left(x+z\right)+3\left(y-z\right)=0 $，即 $ z=2x+3y $，画出约束条件 $ |x|+|y|\leqslant 1 $ 所表示的平面区域，如下图所示：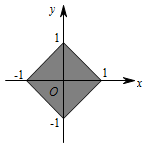
由图可知当 $ x=0 $，$ y=1 $ 时，$ z $ 取最大值 $ 3 $，当 $ x=0 $，$ y=-1 $ 时，$ z $ 取最小值 $ -3 $，故 $ z $ 的取值范围为 $ \left[-3,3\right] $．
由图可知当 $ x=0 $，$ y=1 $ 时，$ z $ 取最大值 $ 3 $，当 $ x=0 $，$ y=-1 $ 时，$ z $ 取最小值 $ -3 $，故 $ z $ 的取值范围为 $ \left[-3,3\right] $．
题目
答案
解析
备注
