已知 $f(x)=x+1$，$g(x)=2^x$，$h(x)=-x+6$，设函数 $F(x)=\min \{f(x),g(x),h(x)\}$，则 $F(x)$ 的最大值是 \((\qquad)\)
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高一（一试）
【标注】
【答案】
C
【解析】
函数 $F(x)$ 的图象如图．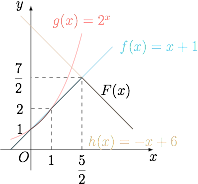
因此 $F(x)$ 的最大值为$$F\left(\dfrac 52\right)=\dfrac 72.$$
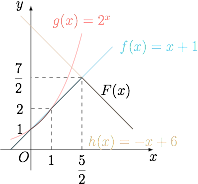因此 $F(x)$ 的最大值为$$F\left(\dfrac 52\right)=\dfrac 72.$$
题目
答案
解析
备注
