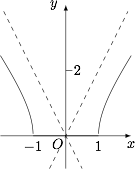
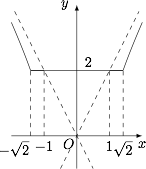
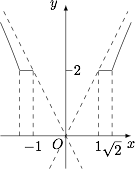
函数 $y=\sqrt{x^2+2\sqrt{x^2-1}}+\sqrt{x^2-2\sqrt{x^2-1}}$ 的图象大致是 \((\qquad)\)
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高二(二试)
【标注】
【答案】
C
【解析】
根据题意$$\begin{split} f(x)&=\sqrt{(x^2-1)+2\sqrt{x^2-1}+1}+\sqrt{x^2-1-2\sqrt{x^2-1}+1}\\
&=\sqrt{\left(\sqrt{x^2-1}+1\right)^2}+\sqrt{\left(\sqrt{x^2-1}-1\right)^2}\\
&=\left(\sqrt{x^2-1}+1\right)+\left|\sqrt{x^2-1}-1\right|,\end{split}$$即有$$f(x)=\begin{cases} 2\sqrt{x^2-1},&|x|\geqslant \sqrt2,\\ 2,&1\leqslant |x|<\sqrt2,
\end{cases}$$因此正确选项为 C.
&=\sqrt{\left(\sqrt{x^2-1}+1\right)^2}+\sqrt{\left(\sqrt{x^2-1}-1\right)^2}\\
&=\left(\sqrt{x^2-1}+1\right)+\left|\sqrt{x^2-1}-1\right|,\end{split}$$即有$$f(x)=\begin{cases} 2\sqrt{x^2-1},&|x|\geqslant \sqrt2,\\ 2,&1\leqslant |x|<\sqrt2,
\end{cases}$$因此正确选项为 C.
题目
答案
解析
备注