已知三棱锥 $V-ABC$，$VA\parallel$ 平面 $\alpha$，$\alpha$ 依次交 $AB,AC,VC,VB$ 于点 $E,F,G,H$，若 $AB=3AE$，并且 $EF\parallel BC$，则多面体 $AFE-VGH$ 与多面体 $EHB-FGC$ 的体积之比为 \((\qquad)\) 
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高二（二试）
【标注】
【答案】
A
【解析】
作 $HI\parallel AV$ 交于 $I$，连接 $IG$，则 $IHG\parallel ABC$．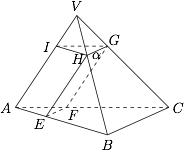
根据题意，有\[\begin{split} V_{AFE-VGH}&=V_{V-IHG}+V_{IHG-AEF}\\
&=\dfrac 1{27}V_{V-ABC}+\dfrac 2{9}V_{V-ABC}\\
&=\dfrac{7}{27}V_{V-ABC}\\
&=\dfrac{7}{20}V_{EHB-FGC}.\end{split}\]
根据题意，有\[\begin{split} V_{AFE-VGH}&=V_{V-IHG}+V_{IHG-AEF}\\&=\dfrac 1{27}V_{V-ABC}+\dfrac 2{9}V_{V-ABC}\\
&=\dfrac{7}{27}V_{V-ABC}\\
&=\dfrac{7}{20}V_{EHB-FGC}.\end{split}\]
题目
答案
解析
备注
