给定圆 $O$ 及圆内一点 $P$．设 $A,B$ 是圆 $O$ 上的两个动点，满足 $\angle APB=90^\circ$，则 $AB$ 的中点的轨迹为 \((\qquad)\)
【难度】
【出处】
2017年清华大学自主招生暨领军计划试题
【标注】
【答案】
A
【解析】
如图，设 $P$ 关于线段 $AB$ 的中点 $M$ 的对称点为 $Q$，连接 $OA,OB,OP,OQ$．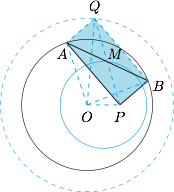
根据题意，$PAQB$ 为矩形，由矩形的性质可得\[OP^2+OQ^2=OA^2+OB^2,\]于是 $OQ$ 为定值，点 $Q$ 的轨迹是以 $O$ 为圆心的圆．进而 $M$ 的轨迹是以 $OP$ 的中点为圆心的圆，其半径为 $\dfrac 12\sqrt{2r^2-d^2}$，其中 $r,d$ 分别为圆 $O$ 的半径以及 $PO$ 的长．
根据题意，$PAQB$ 为矩形，由矩形的性质可得\[OP^2+OQ^2=OA^2+OB^2,\]于是 $OQ$ 为定值，点 $Q$ 的轨迹是以 $O$ 为圆心的圆．进而 $M$ 的轨迹是以 $OP$ 的中点为圆心的圆，其半径为 $\dfrac 12\sqrt{2r^2-d^2}$，其中 $r,d$ 分别为圆 $O$ 的半径以及 $PO$ 的长．
题目
答案
解析
备注
