查看数据源：5a03f77be1d4630009e6d3d4
已知 $F$ 为椭圆 $C:x^2+4y^2=4$ 的左焦点．设 $P$ 是椭圆 $C$ 的右准线上一点，过 $P$ 作椭圆 $C$ 的两条切线 $PA,PB$，切点分别为 $A,B$，则 \((\qquad)\)
A: $\left|AB\right|$ 的最小值为 $\dfrac 12$
B: $\left|AB\right|$ 的最小值为 $1$
C: $\triangle FAB$ 的面积为定值
D: $\triangle FAB$ 的周长为定值
【难度】
【出处】
2017年清华大学自主招生暨领军计划试题
【标注】
  • 知识点
    >
    解析几何
    >
    直线与圆锥曲线
    >
    极点极线的对偶性质
  • 知识点
    >
    解析几何
    >
    椭圆
    >
    椭圆的几何量
    >
    椭圆的通径
  • 题型
    >
    解析几何
    >
    圆锥曲线中的参数取值及范围问题
  • 题型
    >
    解析几何
    >
    圆锥曲线的定点定值问题
【答案】
BD
【解析】
如图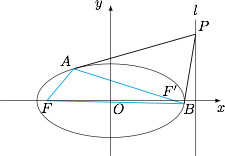．根据极点极线的对偶性质，$AB$ 恒过右焦点 $F'$，于是 $|AB|$ 的最小值为通径长 $1$，$\triangle FAB$ 的周长为定值 $8$．考虑到当 $P$ 的纵坐标趋于无穷大时，$AB$ 趋于椭圆的长轴，因此 $\triangle FAB$ 的面积必然不为定值．
题目 答案 解析 备注
0.107999s