已知平面 $\alpha $ 截一球面得圆 $M$,过圆心 $M$ 且与 $\alpha $ 成 $60^\circ $ 二面角的平面 $\beta $ 截该球面得圆 $N$.若该球面的半径为 $ 4 $,圆 $M$ 的面积为 $4{\mathrm{\pi }}$,则圆 $N$ 的面积为 \((\qquad)\)
【难度】
【出处】
2011年高考大纲全国卷(理)
【标注】
【答案】
D
【解析】
如图所示,设球的半径为 $R$,由圆 $M$ 的面积为 $4{\mathrm{\pi }}$ 知,\[AM = 2,\]球心 $O$ 到圆 $M$ 的距离\[OM = 2\sqrt 3 ,\]在 ${\rm{Rt}}\triangle OMN$ 中,$\angle OMN = 30^\circ $,所以\[ON = \dfrac{1}{2}OM = \sqrt 3,\]故圆 $N$ 的半径\[r = \sqrt {{R^2} - O{N^2}} = \sqrt {13},\]所以圆 $N$ 的面积为\[S = {\mathrm{\pi }}{r^2} = 13{\mathrm{\pi }}.\]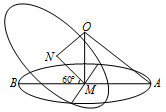

题目
答案
解析
备注