已知直二面角 $\alpha - l - \beta $，点 $A \in \alpha $，$AC \perp l$，$C$ 为垂足，$B \in \beta $，$BD \perp l$，$D$ 为垂足．若 $AB = 2$，$AC = BD = 1$，则 $D$ 到平面 $ABC$ 的距离等于 \((\qquad)\)
【难度】
【出处】
2011年高考大纲全国卷（理）
【标注】
【答案】
C
【解析】
如图，过 $D$ 作 $DE \perp BC$，垂足为 $E$，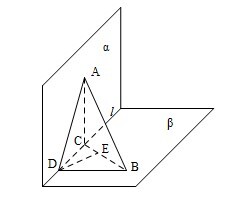
因为 $\alpha - l - \beta $ 是直二面角，
$AC \perp l$，∴ $AC \perp $ 平面 $\beta $，
∴ $AC \perp DE$，$BC \perp DE$，$AC \cap BC = C$，
∴ $DE \perp $ 平面 $ABC$，故 $DE$ 的长为点 $D$ 到平面 $ABC$ 的距离．
在 ${ \mathrm {Rt} }\triangle BCD$ 中，由等面积法得 $DE = \dfrac{BD \times CD}{BC}$，
又 $BC = \sqrt {A{B^2} - A{C^2}} = \sqrt 3 $，$CD = \sqrt {B{C^2} - B{D^2}} = \sqrt 2 $，
∴ $DE = \dfrac{1 \times \sqrt 2 }{\sqrt 3 } = \dfrac{\sqrt 6 }{3}$．
因为 $\alpha - l - \beta $ 是直二面角，$AC \perp l$，∴ $AC \perp $ 平面 $\beta $，
∴ $AC \perp DE$，$BC \perp DE$，$AC \cap BC = C$，
∴ $DE \perp $ 平面 $ABC$，故 $DE$ 的长为点 $D$ 到平面 $ABC$ 的距离．
在 ${ \mathrm {Rt} }\triangle BCD$ 中，由等面积法得 $DE = \dfrac{BD \times CD}{BC}$，
又 $BC = \sqrt {A{B^2} - A{C^2}} = \sqrt 3 $，$CD = \sqrt {B{C^2} - B{D^2}} = \sqrt 2 $，
∴ $DE = \dfrac{1 \times \sqrt 2 }{\sqrt 3 } = \dfrac{\sqrt 6 }{3}$．
题目
答案
解析
备注
