正方形 $ABCD$ 与点 $P$ 在同一平面内，已知该正方形的边长为 $1$，且 $|PA|^2+|PB|^2=|PC|^2$，则 $|PD|$ 的最大值为 \((\qquad)\)
【难度】
【出处】
2017年北京大学自主招生数学试题
【标注】
【答案】
A
【解析】
如图建系，$A(0,0)$，$B(1,0)$，$C(1,1)$，$D(0,1)$，$P(x,y)$．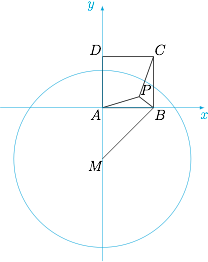
根据题意有\[x^2+y^2+(x-1)^2+y^2=(x-1)^2+(y-1)^2,\]即\[x^2+(y+1)^2=2,\]于是 $P$ 的轨迹是以 $M(0,-1)$ 为圆心，$\sqrt 2$ 为半径的圆，因此 $|PD|$ 的最大值为 $2+\sqrt 2$．
根据题意有\[x^2+y^2+(x-1)^2+y^2=(x-1)^2+(y-1)^2,\]即\[x^2+(y+1)^2=2,\]于是 $P$ 的轨迹是以 $M(0,-1)$ 为圆心，$\sqrt 2$ 为半径的圆，因此 $|PD|$ 的最大值为 $2+\sqrt 2$．
题目
答案
解析
备注
