查看数据源：59ccb1088bc51d0007fbd41f
设函数 $f\left( x \right) = A\sin \left({\omega x + \varphi }\right)$（$A,\omega ,\varphi$ 是常数，$A > 0$，$\omega > 0$）．若 $f\left( x \right)$ 在区间 $\left[{\dfrac{\mathrm \pi} {6},\dfrac{\mathrm \pi} {2}}\right]$ 上具有单调性，且 $f\left({\dfrac{\mathrm \pi} {2}}\right) = f\left({\dfrac{{2{\mathrm \pi} }}{3}}\right) = - f\left({\dfrac{\mathrm \pi} {6}}\right)$，则 $f\left( x \right)$ 的最小正周期为 \((\qquad)\) ．
A: $1$
B: ${\mathrm \pi}$
C: $2\pi$
D: $\dfrac {\mathrm \pi}2$
【难度】
【出处】
2014年高考北京卷（理）
【标注】
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    三角函数
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的周期性
【答案】
B
【解析】
函数 $f(x)$ 的图象经过三个实心点（或空心点），结合 $f(x)$ 在区间 $\left[\dfrac{\pi}6,\dfrac{\pi}2\right]$ 上单调，因此 $x=\dfrac{2\pi}6$ 是函数 $f(x)$ 的零点．又 $f\left(\dfrac{3\pi}6\right)=f\left(\dfrac{4\pi}6\right)$，因此 $x=\dfrac{7\pi}{12}$ 是函数 $f(x)$ 的对称轴，如图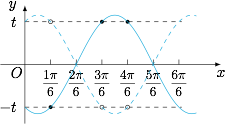．于是 $\dfrac{T}4=\dfrac{7\pi}{12}-\dfrac{2\pi}6$，从而 $T=\pi$．
题目 答案 解析 备注
0.182095s