已知函数 $y = f\left(x\right)$ 的周期为 $2$，当 $x \in \left[ - 1,1\right]$ 时 $f\left(x\right) = {x^2}$，那么函数 $y = f\left(x\right)$ 的图象与函数 $y = |\lg x|$ 的图象的交点共有 \((\qquad)\)
【难度】
【出处】
2011年高考新课标全国卷（文）
【标注】
【答案】
A
【解析】
函数 $y=f\left(x\right)$ 的图象与 $y=\lg x$ 的图象如下图所示：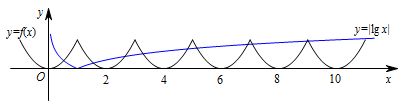
$y=f\left(x\right)$ 的最大值为 $1$，当 $x=10$ 时，$|\lg 9|<1=f\left(9\right)$，当 $x=11$ 时，$|\lg {11}|>f\left(11\right)=1$，所以两个函数图象有 $10$ 个交点．
$y=f\left(x\right)$ 的最大值为 $1$，当 $x=10$ 时，$|\lg 9|<1=f\left(9\right)$，当 $x=11$ 时，$|\lg {11}|>f\left(11\right)=1$，所以两个函数图象有 $10$ 个交点．
题目
答案
解析
备注
