已知 $f(x)$ 是定义在 $\mathbb R$ 上的奇函数，$f(x+2)=f(x)$，当 $x\in (0,1]$ 时，$f(x)=1-2\left|x-\dfrac 12\right|$，则 $f\left(f(x)\right)=\dfrac{5}{4(x-1)}$ 在区间 $[-1,3]$ 内的所有不等实根之和为 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
函数 $f(x)$ 周期为 $2$，且为奇函数，所以 $f(f(x))$ 也是周期为 $2$ 的奇函数，作出它在 $[0,1]$ 上的图象即可得到 $[-1,3]$ 上 $f(f(x))$ 的图象：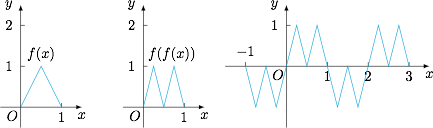
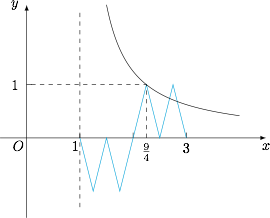
再考虑 $g(x)=\dfrac 5{4(x-1)}$ 的图象，因为它是关于 $(1,0)$ 中心对称的，所以两个函数的交点关于 $(1,0)$ 中心对称，关键是求出交点的个数，只需要考虑 $(1,3]$ 即可，因为$$g\left(\dfrac 94\right)=1=f\left(f\left(\dfrac 94\right)\right),$$所以两个函数在 $(1,3]$ 上有三个交点，从而实根之和为 $3\times 2=6$．
再考虑 $g(x)=\dfrac 5{4(x-1)}$ 的图象，因为它是关于 $(1,0)$ 中心对称的，所以两个函数的交点关于 $(1,0)$ 中心对称，关键是求出交点的个数，只需要考虑 $(1,3]$ 即可，因为$$g\left(\dfrac 94\right)=1=f\left(f\left(\dfrac 94\right)\right),$$所以两个函数在 $(1,3]$ 上有三个交点，从而实根之和为 $3\times 2=6$．
题目
答案
解析
备注
