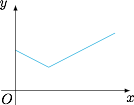
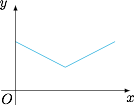
如图，$P$ 是正方体 $ABCD-A_1B_1C_1D_1$ 对角线 $AC_1$ 上一动点，设 $AP$ 的长度为 $x$，若 $\triangle{PBD}$ 的面积为 $f(x)$，则 $f(x)$ 的图象大致是 \((\qquad)\) 
A:
B:
C:
D:
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
如图，设 $O$ 为底面中心，则根据题意$$f(x)=\dfrac 12 |BD|\cdot |OP|.$$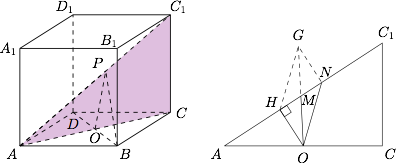
研究平面 $ACC_1$，设 $OH\perp AC_1$．
显然 $|OP|$ 随着 $P$ 从 $A$ 到 $C_1$ 的运动先减小后增大，且在 $H$ 处取得最小值，由于 $H$ 点并不是 $AC_1$ 的中点，因此排除C，D．
接下来研究 $f(x)$ 是否是线性的．
如右图，设 $M$，$N$ 是线段 $HC_1$ 上两点，且 $HM=MN$，则若 $f(x)$ 是线性的，则$$|OM|-|OH|=|ON|-|OM|,$$即$$|OH|+|ON|=2|OM|.$$倍长 $OM$ 至 $G$，则 $2|OM|=|OG|$，显然$$|OH|+|ON|=|OH|+|HG|>|OG|,$$因此 $f(x)$ 不是线性的．
综上，选A．
研究平面 $ACC_1$，设 $OH\perp AC_1$．显然 $|OP|$ 随着 $P$ 从 $A$ 到 $C_1$ 的运动先减小后增大，且在 $H$ 处取得最小值，由于 $H$ 点并不是 $AC_1$ 的中点，因此排除C，D．
接下来研究 $f(x)$ 是否是线性的．
如右图，设 $M$，$N$ 是线段 $HC_1$ 上两点，且 $HM=MN$，则若 $f(x)$ 是线性的，则$$|OM|-|OH|=|ON|-|OM|,$$即$$|OH|+|ON|=2|OM|.$$倍长 $OM$ 至 $G$，则 $2|OM|=|OG|$，显然$$|OH|+|ON|=|OH|+|HG|>|OG|,$$因此 $f(x)$ 不是线性的．
综上，选A．
题目
答案
解析
备注
