在扇形 $OAB$ 中，$\angle AOB=\dfrac{\pi}2$，$OA=1$，点 $C$ 为 弧 $AB$ 上的动点且不与 $A,B$ 重合，$OD\perp BC$ 于 $D$，$OE\perp AC$ 于 $E$，则 \((\qquad)\) 
【难度】
【出处】
2017年清华大学自主招生暨领军计划试题
【标注】
【答案】
ABCD
【解析】
设 $O(0,0)$，$A(0,1)$，$B(1,0)$，$C(\cos x,\sin x)$，则根据圆的垂径定理，有\[D\left(\dfrac{1+\cos x}2,\dfrac{\sin x}2\right),E\left(\dfrac{\cos x}2,\dfrac{1+\sin x}2\right),\]因此\[DE=\sqrt{\left(\dfrac{1+\cos x}2-\dfrac{\cos x}2\right)^2+\left(\dfrac{\sin x}2-\dfrac{1+\sin x}2\right)^2}=\dfrac{\sqrt 2}2,\]选项 A 正确．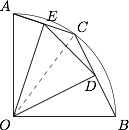
连接 $OC$，则\[\angle DOE=\angle COE+\angle COD=\dfrac 12\angle COA+\dfrac 12\angle COB=\dfrac 12\angle AOB=\dfrac{\pi}4,\]选项 B 正确．
由于 $\triangle DOE$ 中边 $DE$ 和其所对的角均为定值，因此当 $OD=OE$ 时其面积最大，此时 $x=\dfrac{\pi}4$，于是 $\triangle DOE$ 的面积最大值为\[\dfrac 12\cdot \sin\dfrac{\pi}4\cdot OD^2= \dfrac 12\cdot \sin\dfrac{\pi}4\cdot \cos^2\dfrac{\pi}8=\dfrac 18\cot\dfrac{\pi}8,\]选项 C 正确．
由于 $\angle DCE=\dfrac{3\pi}4$ 为定值，因此当 $OD=OE$ 相等时，$OC\perp DE$，四边形 $ODCE$ 取得最大值为\[\dfrac 12\cdot OC\cdot DE=\dfrac{\sqrt 2}4,\]因此选项 D 正确．
连接 $OC$，则\[\angle DOE=\angle COE+\angle COD=\dfrac 12\angle COA+\dfrac 12\angle COB=\dfrac 12\angle AOB=\dfrac{\pi}4,\]选项 B 正确．由于 $\triangle DOE$ 中边 $DE$ 和其所对的角均为定值，因此当 $OD=OE$ 时其面积最大，此时 $x=\dfrac{\pi}4$，于是 $\triangle DOE$ 的面积最大值为\[\dfrac 12\cdot \sin\dfrac{\pi}4\cdot OD^2= \dfrac 12\cdot \sin\dfrac{\pi}4\cdot \cos^2\dfrac{\pi}8=\dfrac 18\cot\dfrac{\pi}8,\]选项 C 正确．
由于 $\angle DCE=\dfrac{3\pi}4$ 为定值，因此当 $OD=OE$ 相等时，$OC\perp DE$，四边形 $ODCE$ 取得最大值为\[\dfrac 12\cdot OC\cdot DE=\dfrac{\sqrt 2}4,\]因此选项 D 正确．
题目
答案
解析
备注
