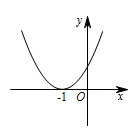
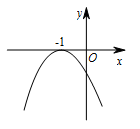
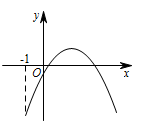
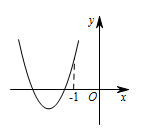
设函数 $f\left( x \right) = a{x^2} + bx + c\left( {a,b,c \in{\mathbb R}} \right)$,若 $x = - 1$ 为函数 $f\left( x \right){{\mathrm e}^x}$ 的一个极值点,则下列图象不可能为 $y = f\left( x \right)$ 图象的是 \((\qquad)\)
【难度】
【出处】
2011年高考浙江卷(文)
【标注】
【答案】
D
【解析】
将 $ f\left(x\right)\mathrm e^x $ 求导,然后将 $ -1 $ 带入导数值得零,从而得到 $ a=c $.
函数 $ f\left(x\right) $ 的图象的对称轴方程为 $ x=-\dfrac b{2a} $,且 $ f\left(-1\right)=2a-b $.
A中,显然 $ f\left(0\right)=c=a>0 $,且 $ f\left(-1\right)=0 $,即 $ b=2a>0 $,不矛盾;
B中,$ f\left(0\right)=c=a<0 $,$ f\left(-1\right)=0,b=2a<0 $,不矛盾;
C中,$ f\left(0\right)=c=a<0 $,$ x=-\dfrac b{2a}>0 $,所以 $ b>0\rightarrow f\left(-1\right)<0 $,不矛盾;
D中,$ f\left(0\right)=c=a>0 $,$ x=-\dfrac b{2a}<-1 $,所以 $ b>2a\rightarrow f\left(-1\right)<0 $,矛盾.
函数 $ f\left(x\right) $ 的图象的对称轴方程为 $ x=-\dfrac b{2a} $,且 $ f\left(-1\right)=2a-b $.
A中,显然 $ f\left(0\right)=c=a>0 $,且 $ f\left(-1\right)=0 $,即 $ b=2a>0 $,不矛盾;
B中,$ f\left(0\right)=c=a<0 $,$ f\left(-1\right)=0,b=2a<0 $,不矛盾;
C中,$ f\left(0\right)=c=a<0 $,$ x=-\dfrac b{2a}>0 $,所以 $ b>0\rightarrow f\left(-1\right)<0 $,不矛盾;
D中,$ f\left(0\right)=c=a>0 $,$ x=-\dfrac b{2a}<-1 $,所以 $ b>2a\rightarrow f\left(-1\right)<0 $,矛盾.
题目
答案
解析
备注