函数 $f\left(x\right) = \sqrt x - \cos x$ 在 $\left[0, + \infty \right)$ 内 \((\qquad)\)
【难度】
【出处】
2011年高考陕西卷(理)
【标注】
【答案】
B
【解析】
令 $f\left(x\right) = \sqrt x - \cos x$ $ = 0$,则 $\sqrt x = \cos x$,函数 $y = \sqrt x $ 和 $y = \cos x$ 在 $\left[0, + \infty \right)$ 的图象如图所示,显然两函数的图象的交点有且只有一个,所以函数 $f\left(x\right) = \sqrt x - \cos x$ 在 $\left[0, + \infty \right)$ 内有且仅有一个零点.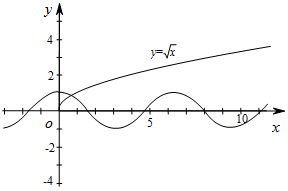

题目
答案
解析
备注