若封闭曲线 $x^4+y^4=1$ 所围成的区域的面积为 $S$，则 \((\qquad)\)
【难度】
【出处】
2008年第十九届“希望杯”全国数学邀请赛高一（二试）
【标注】
【答案】
A
【解析】
如图．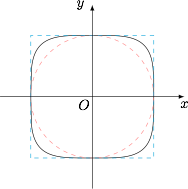
一方面，由于\[\{(x,y)\mid x^4+y^4\leqslant 1\}\subseteq \{(x,y)\mid |x|\leqslant 1,|y|\leqslant 1\},\]于是 $S<4$．
另一方面，由于当 $x^2+y^2=1$ 时，有\[x^4+y^4=1-2x^2y^2\leqslant 1,\]于是\[\{(x,y)\mid x^2+y^2\leqslant 1\}\subseteq\{x,y)\mid x^4+y^4\leqslant 1\},\]因此 $S>\pi$．
一方面，由于\[\{(x,y)\mid x^4+y^4\leqslant 1\}\subseteq \{(x,y)\mid |x|\leqslant 1,|y|\leqslant 1\},\]于是 $S<4$．另一方面，由于当 $x^2+y^2=1$ 时，有\[x^4+y^4=1-2x^2y^2\leqslant 1,\]于是\[\{(x,y)\mid x^2+y^2\leqslant 1\}\subseteq\{x,y)\mid x^4+y^4\leqslant 1\},\]因此 $S>\pi$．
题目
答案
解析
备注
