查看数据源：5a0e7de8aaa1af00079caa08
若集合 $A=\{{x,y}\mid |x|+|y| \leqslant 1\}$，$B=\{{x,y}\mid (y-x)(y+x) \leqslant 0\}$，并且 $M=A\cap B$，则集合 $M$ 构成的图形的面积为  \((\qquad)\)
A: $\dfrac 12$
B: $\sqrt 2$
C: $1$
D: $\dfrac {\sqrt 2}{2}$
【难度】
【出处】
2008年第十九届“希望杯”全国数学邀请赛高一（二试）
【标注】
  • 方法
    >
    数形结合
    >
    不等式(组)的规划
【答案】
C
【解析】
如图，画出集合 $A$，$B$ 表示的平面区域，可得 $M$ 的区域，进而知集合 $M$ 构成的图形的面积为 $1$．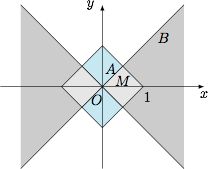
题目 答案 解析 备注
0.120760s