关于 $x$ 的方程 $\left|\mathrm{e}^{|{\ln}x|}-2\right|=t$ $(0<t<1)$，其中 $t$ 是常数，则方程的根的个数是 \((\qquad)\)
【难度】
【出处】
2006年第十七届"希望杯"全国数学邀请赛高二（一试）
【标注】
【答案】
C
【解析】
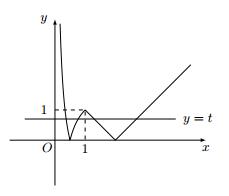$y=\left|\mathrm{e}^{|{\ln}x|}-2\right|$ 的图象如图所示，因此当 $0<t<1$ 时，所以原方程的根的个数为 $4$．
题目
答案
解析
备注
