已知球的直径 $SC = 4$，$A$，$B$ 是该球球面上的两点，$AB = \sqrt 3 $，$\angle ASC = \angle BSC = 30^\circ $，则棱锥 $S - ABC$ 的体积为 \((\qquad)\)
【难度】
【出处】
2011年高考辽宁卷（理）
【标注】
【答案】
C
【解析】
提示：如图，过 $A,B$ 作与 $SC$ 垂直的截面圆 $\odot M$．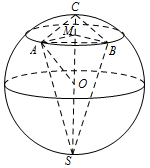
可求得 $AM=BM=AB=\sqrt 3$，所以 $V_{S-ABC}=\dfrac 13S_{\triangle AMB}\cdot SC=\sqrt 3$．
可求得 $AM=BM=AB=\sqrt 3$，所以 $V_{S-ABC}=\dfrac 13S_{\triangle AMB}\cdot SC=\sqrt 3$．
题目
答案
解析
备注
