直线 $y = \dfrac{\sqrt 3 }{3}x + \sqrt 2 $ 与圆心为 $D$ 的圆 $ \begin{cases}
x = \sqrt 3 + \sqrt 3 \cos \theta , \\
y = 1 + \sqrt 3 \sin \theta ,\\
\end{cases} $ $\left( {\theta \in \left[ {0,2{\mathrm \pi }} \right)} \right)$ 交于 $A,B$ 两点，则直线 $AD$ 与 $BD$ 的倾斜角之和为 \((\qquad)\)
x = \sqrt 3 + \sqrt 3 \cos \theta , \\
y = 1 + \sqrt 3 \sin \theta ,\\
\end{cases} $ $\left( {\theta \in \left[ {0,2{\mathrm \pi }} \right)} \right)$ 交于 $A,B$ 两点，则直线 $AD$ 与 $BD$ 的倾斜角之和为 \((\qquad)\)
【难度】
【出处】
2010年高考重庆卷（理）
【标注】
【答案】
C
【解析】
直线与圆如图如示：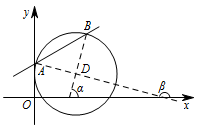
所求的角为 $\alpha+\beta$，计算圆心到直线的距离得 $d=\dfrac{\sqrt 6}{2}$，圆的半径为 $\sqrt 3$，故 $\angle DAB=\dfrac{\mathrm \pi}{4}$．
而 $AB$ 的倾斜角为 $\dfrac{\mathrm \pi}{6}$，故 $\alpha=\dfrac{\mathrm \pi}{4}+\dfrac{\mathrm \pi}{6}=\dfrac{5\mathrm \pi}{12}$，而 $\beta=\alpha+\dfrac{\mathrm \pi}{2}$，故 $ \alpha +\beta =\dfrac{4}{3}{\mathrm \pi} $．
所求的角为 $\alpha+\beta$，计算圆心到直线的距离得 $d=\dfrac{\sqrt 6}{2}$，圆的半径为 $\sqrt 3$，故 $\angle DAB=\dfrac{\mathrm \pi}{4}$．而 $AB$ 的倾斜角为 $\dfrac{\mathrm \pi}{6}$，故 $\alpha=\dfrac{\mathrm \pi}{4}+\dfrac{\mathrm \pi}{6}=\dfrac{5\mathrm \pi}{12}$，而 $\beta=\alpha+\dfrac{\mathrm \pi}{2}$，故 $ \alpha +\beta =\dfrac{4}{3}{\mathrm \pi} $．
题目
答案
解析
备注
