如图，点 $P$ 是正方体 $ABCD$ 外的一点，过点 $P$ 作直线 $l$，记直线 $l$ 与直线 $AC_1,BC$ 的夹角分别为 $\theta_1,\theta_2$，若 $\sin\left(\theta_1-50^\circ\right)=\cos\left(140^\circ-\theta_2\right)=\dfrac 12$，则满足条件的直线 $l$ 的条数为 \((\qquad)\) 
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
易知 $\theta_1=\theta_2=80^\circ$，而 $AC_1$ 与 $BC$ 所成的角为 $\arctan\sqrt 2$，且\[45^\circ<\arctan\sqrt 2<60^\circ.\]题意即过空间一点 $P$ 且与所成角为 $\arctan\sqrt 2$ 的两条直线所成角均为 $80^\circ$ 的直线条数．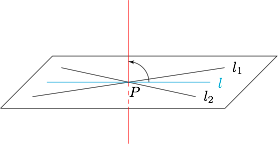
将所有直线都平移，使之都过点 $P$，如图．设 $\langle l_1,l_2\rangle =\arctan \sqrt 2$，取 $l_1,l_2$ 的一条角平分线将其绕 $P$ 点旋转至与 $l_1,l_2$ 都垂直，则在旋转过程中 $l$ 与 $l_1,l_2$ 所成的角始终相等，且从 $\dfrac 12\arctan\sqrt 2$ 变化到 $90^\circ$．类似的，取 $l_1,l_2$ 的另一条角平分线（在 $l_1,l_2$ 所确定的平面内且与如图所示角平分线垂直），则旋转过程中 $l$ 与 $l_1,l_2$ 所成的角始终相等，且从 $90^\circ-\dfrac 12\arctan\sqrt 2$ 变化到 $90^\circ$．考虑到\[\dfrac 12\arctan\sqrt 2<80^\circ,90^\circ-\dfrac 12\arctan\sqrt 2<80^\circ,\]因此两个旋转过程中都存在符合题意的直线．结合对称性可知，满足条件的直线共有 $4$ 条．
将所有直线都平移，使之都过点 $P$，如图．设 $\langle l_1,l_2\rangle =\arctan \sqrt 2$，取 $l_1,l_2$ 的一条角平分线将其绕 $P$ 点旋转至与 $l_1,l_2$ 都垂直，则在旋转过程中 $l$ 与 $l_1,l_2$ 所成的角始终相等，且从 $\dfrac 12\arctan\sqrt 2$ 变化到 $90^\circ$．类似的，取 $l_1,l_2$ 的另一条角平分线（在 $l_1,l_2$ 所确定的平面内且与如图所示角平分线垂直），则旋转过程中 $l$ 与 $l_1,l_2$ 所成的角始终相等，且从 $90^\circ-\dfrac 12\arctan\sqrt 2$ 变化到 $90^\circ$．考虑到\[\dfrac 12\arctan\sqrt 2<80^\circ,90^\circ-\dfrac 12\arctan\sqrt 2<80^\circ,\]因此两个旋转过程中都存在符合题意的直线．结合对称性可知，满足条件的直线共有 $4$ 条．
题目
答案
解析
备注
