查看数据源：59c71e7a778d4700085f6bd3
点 $P(x,y)$ 是曲线 $C:y=\dfrac 1x$（$x>0$）上的一个动点，曲线 $C$ 在点 $P$ 处的切线与 $x$ 轴、$y$ 轴分别交于 $A,B$ 两点，点 $O$ 是坐标原点，则 \((\qquad)\)
A: $|PA|=|PB|$
B: $\triangle OAB$ 的面积为定值
C: 曲线 $C$ 上存在两点 $M,N$ 使得 $\triangle OMN$ 是等边三角形
D: 曲线 $C$ 上存在两点 $M,N$ 使得 $\triangle OMN$ 是等腰直角三角形
【难度】
【出处】
无
【标注】
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的零点
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    反比例函数
  • 方法
    >
    思考方式
    >
    构造状态量
【答案】
ABCD
【解析】
选项A先证明一个引理．
引理若直线 $l$ 是曲线 $C:y=\dfrac 1x$ 的割线，且割点分别为 $P,Q$，直线 $l$ 与 $x$ 轴、$y$ 轴分别交于 $A,B$ 两点，则 $PB=QA$，如图．证明过 $P,Q$ 作两坐标轴的垂线，设 $PM$ 与 $x$ 轴垂直且相交于 $M$，$QN$ 与 $y$ 轴垂直且相交于 $N$，$PM$ 与 $QN$ 相交于 $R$，则根据反比例函数图象的性质，有 $S_{\triangle NPR}=S_{\triangle MQR}$，因此\[S_{\triangle NPQ}=S_{\triangle MPQ},\]进而 $MN\parallel PQ$，从而 $BP,NM,QA$ 平行且相等，于是引理得证．
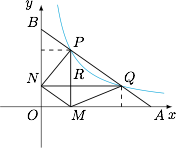
根据引理，当 $P,Q$ 重合时，割线变成切线，此时有 $|PA|=|PB|$，命题成立．
选项B由于 $|PA|=|PB|$，因此 $\triangle OAB$ 的面积为定值 $2$．
选项C在曲线 $C$ 上选取关于 $y=x$ 对称的两点 $M,N$，形成等腰 $\triangle OMN$，当 $N$ 从 $(1,0)$ 向 $(+\infty,0)$ 运动时，$\triangle OMN$ 的顶角 $\angle MON$ 从 $0$ 增大到 $90^\circ$，在运动的过程中必然存在 $\triangle MON$ 为 $60^\circ$ 的时刻，此时 $\triangle MON$ 为等边三角形，命题正确．选项D过 $O$ 作射线 $OM$，与曲线 $C$ 交于 $M$．将射线 $OM$ 顺时针旋转 $45^\circ$ 得到射线 $ON$，与曲线 $C$ 交于 $N$．当 $M$ 从 $(0,+\infty)$ 运动到 $(1,1)$ 时，$ \dfrac{OM}{ON} $ 的值从 $ +\infty $ 变化到 $ 0 $，在运动的过程中必然存在 $ \dfrac{OM}{ON} $ 为 $ \sqrt 2 $ 和 $ \dfrac{\sqrt 2}2 $ 的时刻，此时 $ \triangle MON $ 为等腰直角三角形，命题正确．
题目 答案 解析 备注
0.113706s