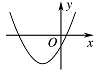
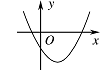
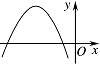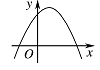设 $abc > 0$,二次函数 $f\left(x\right) = a{x^2} + bx + c$ 的图象可能是 \((\qquad)\)
【难度】
【出处】
2010年高考安徽卷(理)
【标注】
【答案】
D
【解析】
由 $ A、C、D$ 知,$f\left( 0 \right) = c < 0$,因为 $ abc>0 $,那么 $ ab<0 $,从而对称轴 $x=- \dfrac{b}{{2a}} >0$,由此 $ A、C$ 错误,$D$ 符合要求;
由 $ B$ 知,$f\left( 0 \right) = c > 0$,因为 $ abc>0 $,那么 $ ab>0 $,从而对称轴 $x=- \dfrac{b}{{2a}} <0$,由此 $ B$ 错误.
由 $ B$ 知,$f\left( 0 \right) = c > 0$,因为 $ abc>0 $,那么 $ ab>0 $,从而对称轴 $x=- \dfrac{b}{{2a}} <0$,由此 $ B$ 错误.
题目
答案
解析
备注