如图，在边长为 $\sqrt 3$ 的菱形 $ABCD$ 中，$\angle DAB=\dfrac{\pi}3$，$DE=\dfrac 12EC$，$F$ 为线段 $BC$ 的中点，$G$ 为 $EF$ 上的一点，且 $\overrightarrow{AG}=\dfrac 12\overrightarrow{AC}+t\overrightarrow{AD}$，则 $\left|\overrightarrow{BG}\right|$ 的值是 \((\qquad)\) 
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
如图建系，设菱形 $ABCD$ 对角线的交点为 $O$，则 $\overrightarrow{AO}=\dfrac 12\overrightarrow{AC}$，因此 $OG\parallel AD$．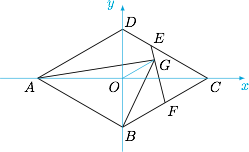
此时 $A\left(-\dfrac 32,0\right)$，$B\left(0,-\dfrac{\sqrt 3}2\right)$，$C\left(\dfrac 32,0\right)$，$D\left(0,\dfrac{\sqrt 3}2\right)$，进而\[E\left(\dfrac 12,\dfrac{\sqrt 3}3\right),F\left(\dfrac 34,-\dfrac{\sqrt 3}4\right),\]于是\[EF:y=-\dfrac{7\sqrt 3}3x+\dfrac{3\sqrt 3}2,\]而\[OG:y=\dfrac{\sqrt 3}3x,\]联立解得 $G\left(\dfrac 9{16},\dfrac{3\sqrt 3}{16}\right)$，因此\[BG=\sqrt{\left(\dfrac{9}{16}-0\right)^2+\left(\dfrac{3\sqrt 3}{16}+\dfrac{\sqrt 3}2\right)^2}=\dfrac{\sqrt{111}}8.\]
此时 $A\left(-\dfrac 32,0\right)$，$B\left(0,-\dfrac{\sqrt 3}2\right)$，$C\left(\dfrac 32,0\right)$，$D\left(0,\dfrac{\sqrt 3}2\right)$，进而\[E\left(\dfrac 12,\dfrac{\sqrt 3}3\right),F\left(\dfrac 34,-\dfrac{\sqrt 3}4\right),\]于是\[EF:y=-\dfrac{7\sqrt 3}3x+\dfrac{3\sqrt 3}2,\]而\[OG:y=\dfrac{\sqrt 3}3x,\]联立解得 $G\left(\dfrac 9{16},\dfrac{3\sqrt 3}{16}\right)$，因此\[BG=\sqrt{\left(\dfrac{9}{16}-0\right)^2+\left(\dfrac{3\sqrt 3}{16}+\dfrac{\sqrt 3}2\right)^2}=\dfrac{\sqrt{111}}8.\]
题目
答案
解析
备注
