设不等式组 $ {\begin{cases}
{{x}} + y - 11 \geqslant 0, \\
3x - y + 3 \geqslant 0, \\
5x - 3y +9 \leqslant 0 ,\\
\end{cases}} $ 表示的平面区域为 $ D $,若指数函数 $ y= {a^x} $ 的图象上存在区域 $ D $ 上的点,则 $ a $ 的取值范围是 \((\qquad)\)
{{x}} + y - 11 \geqslant 0, \\
3x - y + 3 \geqslant 0, \\
5x - 3y +9 \leqslant 0 ,\\
\end{cases}} $ 表示的平面区域为 $ D $,若指数函数 $ y= {a^x} $ 的图象上存在区域 $ D $ 上的点,则 $ a $ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2010年高考北京卷(理)
【标注】
【答案】
A
【解析】
作出不等式组 $\left\{ {\begin{array}{*{20}{c}}
{x + y - 11 \geqslant 0}, \\
{3x - y + 3 \geqslant 0}, \\
{5x - 3y + 9 \leqslant 0}
\end{array}} \right.$ 所表示的平面区域 $ D $,如图阴影部分所示,要使指数函数 $ y=a^x $ 的图象上存在区域 $ D $ 上的点,则有 $ a>1 $,当指数函数 $ y=a^x $ 的图象过点 $ B\left(2,9\right) $ 时,相应的 $ a $ 值最大,此时 $ a=3 $,即 $ a\in \left(1,3\right] $.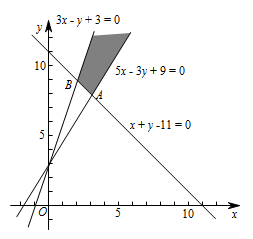
{x + y - 11 \geqslant 0}, \\
{3x - y + 3 \geqslant 0}, \\
{5x - 3y + 9 \leqslant 0}
\end{array}} \right.$ 所表示的平面区域 $ D $,如图阴影部分所示,要使指数函数 $ y=a^x $ 的图象上存在区域 $ D $ 上的点,则有 $ a>1 $,当指数函数 $ y=a^x $ 的图象过点 $ B\left(2,9\right) $ 时,相应的 $ a $ 值最大,此时 $ a=3 $,即 $ a\in \left(1,3\right] $.

题目
答案
解析
备注