查看数据源：5a0940148621cc0009c5fd73
已知某几何体的三视图如图所示，则该几何体的最长棱为 \((\qquad)\)
A: $\sqrt {19}$
B: $\sqrt {22}$
C: $5$
D: $2\sqrt 7$
【难度】
【出处】
2017年清华大学THUSSAT测试理科数学（一测）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的三视图
【答案】
B
【解析】
根据三视图，可得该几何体的直观图如下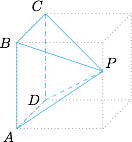．因此该四棱锥 $P-ABCD$ 的最长棱为\[PD=\sqrt{2^2+3^2+3^2}=\sqrt {22}.\]
题目 答案 解析 备注
0.112589s