在直三棱柱 $A_{1}B_{1}C_{1}-ABC$ 中，$\angle BAC=\dfrac{\pi}{2}$，$AB=AC=AA_{1}=1$．已知 $G$ 与 $E$ 分别为 $A_{1}B_{1}$ 和 $CC_{1}$ 的中点，$D$ 与 $F$ 分别为线段 $AC$ 和 $AB$ 上的动点（不包括端点）．若 $GD\perp EF$，则线段 $DF$ 的长度的取值范围为 \((\qquad)\)
【难度】
【出处】
2013年全国高中数学联赛黑龙江省预赛
【标注】
【答案】
A
【解析】
如图，建立空间直角坐标系 $A-CBA_1$．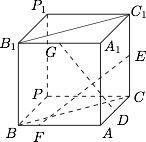
设 $AD=a$，$AF=b$，则有 $D(a,0,0)$，$F(0,b,0)$，$E\left(1,0,\dfrac 12\right)$，$G\left(0,\dfrac 12,1\right)$．于是 $GD\perp EF$ 即\[\left(a,-\dfrac 12,-1\right)\cdot \left(-1,b,-\dfrac 12\right)=0,\]也即\[2a+b=1.\]因此\[DF^2=a^2+b^2=a^2+(1-2a)^2=5a^2-4a+1,\]考虑到 $a$ 的取值范围是 $\left(0,\dfrac 12\right)$，于是 $DF^2$ 的取值范围是 $\left(\dfrac 15,1\right)$．
设 $AD=a$，$AF=b$，则有 $D(a,0,0)$，$F(0,b,0)$，$E\left(1,0,\dfrac 12\right)$，$G\left(0,\dfrac 12,1\right)$．于是 $GD\perp EF$ 即\[\left(a,-\dfrac 12,-1\right)\cdot \left(-1,b,-\dfrac 12\right)=0,\]也即\[2a+b=1.\]因此\[DF^2=a^2+b^2=a^2+(1-2a)^2=5a^2-4a+1,\]考虑到 $a$ 的取值范围是 $\left(0,\dfrac 12\right)$，于是 $DF^2$ 的取值范围是 $\left(\dfrac 15,1\right)$．
题目
答案
解析
备注
