当 $x\in \mathbb R$ 时，函数 $y=\sqrt{x^2+2x+10}-\sqrt{x^2-x+10}$ \((\qquad)\)
【难度】
【出处】
2007年第十八届"希望杯"全国数学邀请赛高二（二试）
【标注】
【答案】
C
【解析】
因为$$\begin{split} y&=\sqrt{x^2+2x+10}-\sqrt{x^2-x+10}\\
&=\sqrt{(x+1)^2+9}-\sqrt{\left(x-\dfrac12\right)^2+\dfrac{39}4}.\end{split}$$记 $P(x,0)$，$A(-1,3)$，$B\left(\dfrac 12,\dfrac{\sqrt{39}}2\right)$，则\[y=PA-PB.\]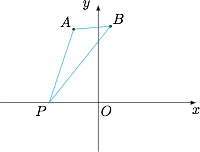
一方面，有\[PA-PB\geqslant -AB,\]等号当 $A$ 位于线段 $PB$ 上时取得等号，因此所求函数有最小值．
另一方面，由于\[y=\dfrac{3x}{\sqrt{x^2+2x+10}+\sqrt{x^2-x+10}},\]于是当 $x\leqslant 0$ 时，有 $y\leqslant 0$；当 $x>0$ 时，有\[y<\dfrac{3x}{x+1+x-\dfrac 12}<\dfrac 32,\]又当 $x\to +\infty$ 时，有 $y\to \dfrac 32$，于是函数没有最大值．
&=\sqrt{(x+1)^2+9}-\sqrt{\left(x-\dfrac12\right)^2+\dfrac{39}4}.\end{split}$$记 $P(x,0)$，$A(-1,3)$，$B\left(\dfrac 12,\dfrac{\sqrt{39}}2\right)$，则\[y=PA-PB.\]
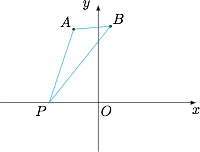一方面，有\[PA-PB\geqslant -AB,\]等号当 $A$ 位于线段 $PB$ 上时取得等号，因此所求函数有最小值．另一方面，由于\[y=\dfrac{3x}{\sqrt{x^2+2x+10}+\sqrt{x^2-x+10}},\]于是当 $x\leqslant 0$ 时，有 $y\leqslant 0$；当 $x>0$ 时，有\[y<\dfrac{3x}{x+1+x-\dfrac 12}<\dfrac 32,\]又当 $x\to +\infty$ 时，有 $y\to \dfrac 32$，于是函数没有最大值．
题目
答案
解析
备注
