设点 $P$ 在 $\triangle{ABC}$ 内，提出以下命题：
① 存在正数 $\lambda_1,\lambda_2$，使 $\overrightarrow{AP}=\lambda_1\overrightarrow{AB}+\lambda_2\overrightarrow{AC}$；
② 如果 $\overrightarrow{AP}\cdot \overrightarrow{BC}=0$ 且 $\overrightarrow{BP}\cdot \overrightarrow{AC}=0$，那么 $\overrightarrow{CP}\cdot \overrightarrow{AB}=0$；
③ 如果 $3\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{AC}$，那么 $3\overrightarrow{BP}=\overrightarrow{BC}+\overrightarrow{BA}$；
④ 如果 $|\overrightarrow{PA}|=|\overrightarrow{PB}|=|\overrightarrow{PC}|$，那么 $\triangle{ABC}$ 是锐角三角形．
在这 $4$ 个命题中，正确命题的个数为 \((\qquad)\)
① 存在正数 $\lambda_1,\lambda_2$，使 $\overrightarrow{AP}=\lambda_1\overrightarrow{AB}+\lambda_2\overrightarrow{AC}$；
② 如果 $\overrightarrow{AP}\cdot \overrightarrow{BC}=0$ 且 $\overrightarrow{BP}\cdot \overrightarrow{AC}=0$，那么 $\overrightarrow{CP}\cdot \overrightarrow{AB}=0$；
③ 如果 $3\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{AC}$，那么 $3\overrightarrow{BP}=\overrightarrow{BC}+\overrightarrow{BA}$；
④ 如果 $|\overrightarrow{PA}|=|\overrightarrow{PB}|=|\overrightarrow{PC}|$，那么 $\triangle{ABC}$ 是锐角三角形．
在这 $4$ 个命题中，正确命题的个数为 \((\qquad)\)
【难度】
【出处】
2007年第十八届“希望杯”全国数学邀请赛高一（二试）
【标注】
【答案】
D
【解析】
对于命题 ①，由于 $\overrightarrow{AB},\overrightarrow{AC}$ 形成一组基底，于是命题成立．
对于命题 ②，若 $\overrightarrow {AP}\cdot \overrightarrow{BC}=0$，则 $AP\perp BC$，同理有 $BP\perp AC$，则 $P$ 为 $\triangle{ABC}$ 的垂心，故 $CP\perp AB$，所以\[\overrightarrow{CP}\cdot \overrightarrow{AB}=0.\]对于命题 ③，设 $BC$ 中点为 $M$，若\[3\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{AC},\]则\[\overrightarrow{AP}=\dfrac 23\overrightarrow{AM},\]即 $P$ 为 $\triangle{ABC}$ 的重心，因此\[3\overrightarrow{BP}=\overrightarrow{BC}+\overrightarrow{BA}\]成立．
对于命题 ④，若 $\Big|\overrightarrow{PA}\Big|=\Big|\overrightarrow{PB}\Big|=\Big|\overrightarrow{PC}\Big|$，则 $P$ 为 $\triangle{ABC}$ 的外心，又 $P$ 在 $\triangle{ABC}$ 内部，如图所示．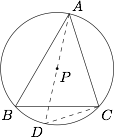
连接 $AP$ 并延长交圆 $P$ 于点 $D$，则 $AD$ 为直径，连接 $DC$，所以 $\angle{ACD}=90^{\circ}$，则\[\angle{D}=\angle{ABC}<90^{\circ},\]同理可证 $\angle{BAC},\angle{ACB}$ 均小于 $90^{\circ}$，即 $\triangle{ABC}$ 为锐角三角形．
对于命题 ②，若 $\overrightarrow {AP}\cdot \overrightarrow{BC}=0$，则 $AP\perp BC$，同理有 $BP\perp AC$，则 $P$ 为 $\triangle{ABC}$ 的垂心，故 $CP\perp AB$，所以\[\overrightarrow{CP}\cdot \overrightarrow{AB}=0.\]对于命题 ③，设 $BC$ 中点为 $M$，若\[3\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{AC},\]则\[\overrightarrow{AP}=\dfrac 23\overrightarrow{AM},\]即 $P$ 为 $\triangle{ABC}$ 的重心，因此\[3\overrightarrow{BP}=\overrightarrow{BC}+\overrightarrow{BA}\]成立．
对于命题 ④，若 $\Big|\overrightarrow{PA}\Big|=\Big|\overrightarrow{PB}\Big|=\Big|\overrightarrow{PC}\Big|$，则 $P$ 为 $\triangle{ABC}$ 的外心，又 $P$ 在 $\triangle{ABC}$ 内部，如图所示．
连接 $AP$ 并延长交圆 $P$ 于点 $D$，则 $AD$ 为直径，连接 $DC$，所以 $\angle{ACD}=90^{\circ}$，则\[\angle{D}=\angle{ABC}<90^{\circ},\]同理可证 $\angle{BAC},\angle{ACB}$ 均小于 $90^{\circ}$，即 $\triangle{ABC}$ 为锐角三角形．
题目
答案
解析
备注
