正方形 $ ABCD $ 的边长为 $ 1 $，点 $ E $ 在边 $ AB $ 上，点 $ F $ 在边 $ BC $ 上，$ AE=BF={\dfrac{3}{7}} $．动点 $ P $ 从 $ E $ 出发沿直线向 $ F $ 运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角，当点 $ P $ 第一次碰到 $ E $ 时，$ P $ 与正方形的边碰撞的次数为 \((\qquad)\)
【难度】
【出处】
2012年高考大纲全国卷（理）
【标注】
【答案】
B
【解析】
如图，$E$ 点对应的点为\[\left(2m\pm\dfrac 37,2n\right),\]其中 $m,n\in\mathbb Z$．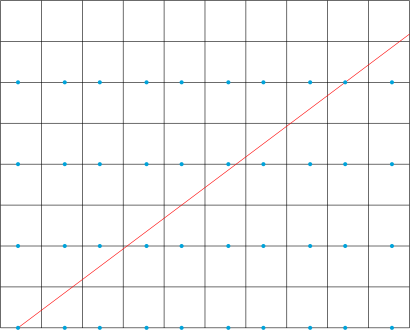
考虑到\[\dfrac{2n-0}{2m\pm \dfrac 37-\dfrac 37}=\dfrac 34,\]即\[2m=3n,\]于是最小的正整数解为 $(m,n)=(3,2)$，对应的碰撞次数为\[2(m+n)=14.\]
考虑到\[\dfrac{2n-0}{2m\pm \dfrac 37-\dfrac 37}=\dfrac 34,\]即\[2m=3n,\]于是最小的正整数解为 $(m,n)=(3,2)$，对应的碰撞次数为\[2(m+n)=14.\]
题目
答案
解析
备注
