三棱柱 $ABC - {A_1}{B_1}{C_1}$ 的底面是边长为 $1$ 的正三角形，高 $A{A_1} = 1$，在 $AB$ 上取一点 $P$，设 $\triangle P{A_1}{C_1}$ 与底面所成的二面角为 $\alpha $，$\triangle P{B_1}{C_1}$ 与底面所成的二面角为 $\beta $，则 $\tan \left( {\alpha + \beta } \right)$ 的最小值是 \((\qquad)\)
【难度】
【出处】
2009年复旦大学自主招生资格选拔测试
【标注】
【答案】
C
【解析】
设 $AP = x$，$BP = 1 - x$，如图．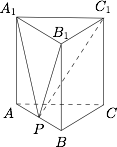
则\[\begin{split} \tan \alpha &= \dfrac{2}{{\sqrt 3 x}},\\
\tan \beta &= \dfrac{2}{{\sqrt 3 \left( {1 - x} \right)}},\end{split}\]于是$$\tan \left( {\alpha + \beta } \right) = \dfrac{{2\sqrt 3 }}{{3x\left( {1 - x} \right) - 4}} \geqslant - \dfrac{{8\sqrt 3 }}{{13}},$$当且仅当 $x = \dfrac{1}{2}$ 时取得等号，因此所求的最小值为 $-\dfrac{8\sqrt 3}{13}$．
则\[\begin{split} \tan \alpha &= \dfrac{2}{{\sqrt 3 x}},\\\tan \beta &= \dfrac{2}{{\sqrt 3 \left( {1 - x} \right)}},\end{split}\]于是$$\tan \left( {\alpha + \beta } \right) = \dfrac{{2\sqrt 3 }}{{3x\left( {1 - x} \right) - 4}} \geqslant - \dfrac{{8\sqrt 3 }}{{13}},$$当且仅当 $x = \dfrac{1}{2}$ 时取得等号，因此所求的最小值为 $-\dfrac{8\sqrt 3}{13}$．
题目
答案
解析
备注
