如图，在长方形 $ABCD$ 中，$AB=2$，$BC=1$，$E$ 为 $DC$ 的中点，$F$ 为线段 $EC$（端点除外）上一动点．现将 $\triangle{AFD}$ 沿 $AF$ 折起，使平面 $ABD\perp $ 平面 $ABC$．在平面 $ABD$ 内过点 $D$ 作 $DK\perp AB$，$K$ 为垂足．设 $AK=t$，则 $t$ 的取值范围是 \((\qquad)\) ．
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
要求 $AK$ 的取值范围，就需要建立 $AK$ 与 $F$ 位置的一个关系式，也即设 $DF=x$（$1<x<2$），求 $t(x)$．
连接 $FK$，要保证 $ABD\perp ABC$，只需要 $DK\perp FK$ 即可．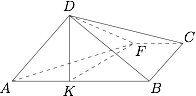
于是$$DK^2+KF^2=DF^2,$$即$$DA^2-AK^2+KF^2=DF^2,$$所以$$1-t^2+(x-t)^2+1^2=x^2,$$故$$t=\dfrac 1x,$$于是 $t$ 的取值范围为 $\left(\dfrac 12 ,1\right)$．
连接 $FK$，要保证 $ABD\perp ABC$，只需要 $DK\perp FK$ 即可．
于是$$DK^2+KF^2=DF^2,$$即$$DA^2-AK^2+KF^2=DF^2,$$所以$$1-t^2+(x-t)^2+1^2=x^2,$$故$$t=\dfrac 1x,$$于是 $t$ 的取值范围为 $\left(\dfrac 12 ,1\right)$．
题目
答案
解析
备注
