对一个棱长为 $1$ 的正方体木块 $ABCD - {A_1}{B_1}{C_1}{D_1}$,在过顶点 ${A_1}$ 的三条棱上分别取点 $E,F,G$,使 ${A_1}E = {A_1}F = {A_1}G$.削掉四面体 ${A_1} - EFG$ 后,以截面 $\triangle EFG$ 为底面,在立方体中打一个三棱柱的洞,使棱柱的侧棱均平行于对角线 ${A_1}C$.当洞打穿后,顶点 $C$ 处消掉后,出口是一个空间多边形,则这个多边形是 \((\qquad)\)
【难度】
【出处】
2008年上海财经大学自主招生试题
【标注】
【答案】
C
【解析】
如图,截面为六边形 $E_1MF_1NG_1PE_1$,其中 $E_1,F_1,G_1$ 分别为 $AC,B_1C,D_1C$ 的三等分点(靠近 $C$),$M,N,P$ 分别为 $BC,C_1C,DC$ 的六等分点(靠近 $C$).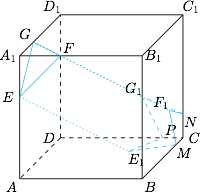

题目
答案
解析
备注