在正方体 $ABCD-A_1B_1C_1D_1$ 中,点 $P$ 在正方体表面运动,$P$ 不与 $A$ 重合,如果 $\triangle ABD_1$ 的面积与 $\triangle PBD_1$ 的面积相等,那么这样的点 $P$ 个数为 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
根据题意,$P$ 点到正方体的体对角线 $BD_1$ 的距离与 $A$ 点到 $BD_1$ 的距离相同,因此 $P$ 点在以 $BD_1$ 为轴,$d(A,BD_1)$ 为半径的圆柱面上.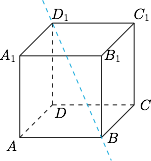 如图,考虑到正方体绕直线 $BD_1$ 旋转形成的曲面由圆锥面和双曲面(异面直线绕其中一条旋转形成)构成,因此公共点共有 $5$ 个,为除 $A,B,D_1$ 以外的正方体的顶点.
如图,考虑到正方体绕直线 $BD_1$ 旋转形成的曲面由圆锥面和双曲面(异面直线绕其中一条旋转形成)构成,因此公共点共有 $5$ 个,为除 $A,B,D_1$ 以外的正方体的顶点.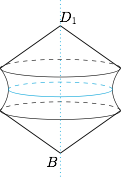
 如图,考虑到正方体绕直线 $BD_1$ 旋转形成的曲面由圆锥面和双曲面(异面直线绕其中一条旋转形成)构成,因此公共点共有 $5$ 个,为除 $A,B,D_1$ 以外的正方体的顶点.
如图,考虑到正方体绕直线 $BD_1$ 旋转形成的曲面由圆锥面和双曲面(异面直线绕其中一条旋转形成)构成,因此公共点共有 $5$ 个,为除 $A,B,D_1$ 以外的正方体的顶点.
题目
答案
解析
备注