设 ${F_1}$、${F_2}$ 分别为双曲线 $\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\left(a>0,b>0\right)$ 的左、右焦点，若在双曲线右支上存在点 $P$，满足 $\left| {P{F_2}} \right| = \left| {{F_1}{F_2}} \right|$，且 ${F_2}$ 到直线 $P{F_1}$ 的距离等于双曲线的实轴长，则该双曲线的渐近线方程为 \((\qquad)\)
【难度】
【出处】
2010年高考浙江卷（理）
【标注】
【答案】
C
【解析】
结合已知条件和双曲线方程中的隐含条件 $ c^2=a^2+b^2 $（$ c$ 为半焦距），得到 $ a $ 与 $ b $ 之间的等量关系，再根据双曲线的几何意义求渐近线方程即可．如图，过 $F_2 $ 作 ${{F_2}M}\perp F_1P$ 于 $M $ 点．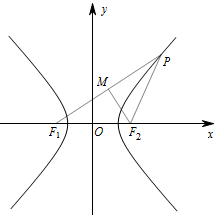
根据题意，得 $\left| {P{F_2}} \right| = \left| {{F_1}{F_2}} \right| = 2c,\left| {{F_2}M} \right| = 2a$．在 $ {\mathrm{ \mathrm {Rt}}} \triangle F_1F_2M$ 中，\[\left| {{F_1}M} \right| = \sqrt {{{\left| {{F_1}{F_2}} \right|}^2} - {{\left| {{F_2}M} \right|}^2}} = \sqrt {4{c^2} - 4{a^2}} = 2b.\]由 $\left| {P{F_1}} \right| - \left| {P{F_2}} \right| = 2a$ 得 $4b - 2c = 2a$，结合 $ c^2=a^2+b^2 $ 消去 $ c$ 得 $3b=4a $，故渐近线方程为 $ 4x\pm 3y=0 $．
根据题意，得 $\left| {P{F_2}} \right| = \left| {{F_1}{F_2}} \right| = 2c,\left| {{F_2}M} \right| = 2a$．在 $ {\mathrm{ \mathrm {Rt}}} \triangle F_1F_2M$ 中，\[\left| {{F_1}M} \right| = \sqrt {{{\left| {{F_1}{F_2}} \right|}^2} - {{\left| {{F_2}M} \right|}^2}} = \sqrt {4{c^2} - 4{a^2}} = 2b.\]由 $\left| {P{F_1}} \right| - \left| {P{F_2}} \right| = 2a$ 得 $4b - 2c = 2a$，结合 $ c^2=a^2+b^2 $ 消去 $ c$ 得 $3b=4a $，故渐近线方程为 $ 4x\pm 3y=0 $．
题目
答案
解析
备注
