查看数据源：599165bb2bfec200011df06b
设函数 $f\left(x\right) = 4\sin \left(2x + 1\right) - x$，则在下列区间中函数 $f\left(x\right)$ 不存在零点的是 \((\qquad)\)
A: $ \left[-4,-2\right] $
B: $ \left[-2,0\right] $
C: $ \left[0,2\right] $
D: $ \left[2,4\right] $
【难度】
【出处】
2010年高考浙江卷（理）
【标注】
【答案】
A
【解析】
分别作出函数 $ h(x)=x $ 与 $ g(x)=4\sin (2x+1) $ 的图象，要使函数 $ f(x) $ 在区间中不存在零点，即两函数 $ h(x)=x $ 与 $ g(x)=4\sin (2x+1) $ 的图象没有交点．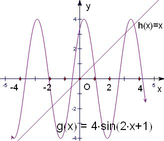
题目 答案 解析 备注
0.166477s